import ipympl
%matplotlib widget
%matplotlib inline
import ipywidgets as widgets
import matplotlib.pyplot as plt
import numpy as np
import sympy as sy
import pandas as pd
from causalgraphicalmodels import CausalGraphicalModel
import os
os.environ["PATH"] += os.pathsep + 'C:/Program Files/Graphviz/bin/'
import warnings
warnings.filterwarnings('ignore')

2. La curva IS (Inversión-Ahorro)#

2.1. Derivación de la curva IS#

La curva IS se deriva de la igualdad entre el ingreso \((Y)\) y la demanda agregada \((DA)\):

\[ Y = C + I + G + X - M \]

Considerando que:

\[ C = C_0 + bY^d \]

\[ I = I_0 - hr \]

\[ G = G_0 \]

\[ T = tY \]

\[ X = X_0 \]

\[ M = mY^d \]

Para llegar al equilibrio Ahorro-Inversión, debemos restar la tributación \((T)\) de ambos miembros de la igualdad.

\[ Y - T = C + I - T + G + X - M \]

\[ Y^d = C + I - T + G + X - M \]

Esta igualdad se puede reescribir de la siguiente forma:

\[ (Y^d - C) + (T - G) + (M - X) = I \]

Las tres partes de la derecha constituyen los tres componentes del ahorro total \( (S) \): ahorro privado \( (S_p) \), ahorro del gobierno \( (S_g) \) y ahorro externo \( (S_e) \):

\[ S = S_p + S_g + S_e \]

Entonces, el ahorro total es igual a la inversión

\[ S_p + S_g + S_e = I \]

\[ S(Y) = I(r) \]

Haciendo reemplazos se obtiene que:

\[ S_p + S_g + S_e = I_0 - hr \]

\[ (Y^d - C_0 - bY^d) + (T - G_0) + (mY^d - X_0) = I_0 - hr \]

Considerando las observaciones anteriores sobre los componentes de la condición de equilibrio \((Y)\):

\[ [1 - (b - m)(1 - t)]Y - (C_0 + G_0 + X_0) = I_0 - hr \]

La curva IS se puede expresar con una ecuación donde la tasa de interés es una función del ingreso:

\[ hr = (C_0 + G_0 + I_0 + X_0) - (1 - (b - m)(1 - t))Y \]

\[ r = \frac{1}{h}(C_0 + G_0 + I_0 + X_0) - \frac{1 - (b - m)(1 - t)}{h}Y \]

Y puede simplificarse en:

\[ r = \frac{B_0}{h} - \frac{B_1}{h}Y \]

Donde \( B_0 = C_0 + G_0 + I_0 + X_0 \) es el intercepto y \( B_1 = 1 - (b - m)(1 - t) \) es la pendiente.

Y la curva IS se grafica de la siguiente manera:

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

# Gráfico de la curva IS

# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "#8B0A50") #Demanda agregada

# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())   
ax.xaxis.set_major_locator(plt.NullLocator())

# Título, ejes y leyenda
ax.set(title = "Curva IS", xlabel= 'Y', ylabel= 'r')
ax.legend()

plt.show()

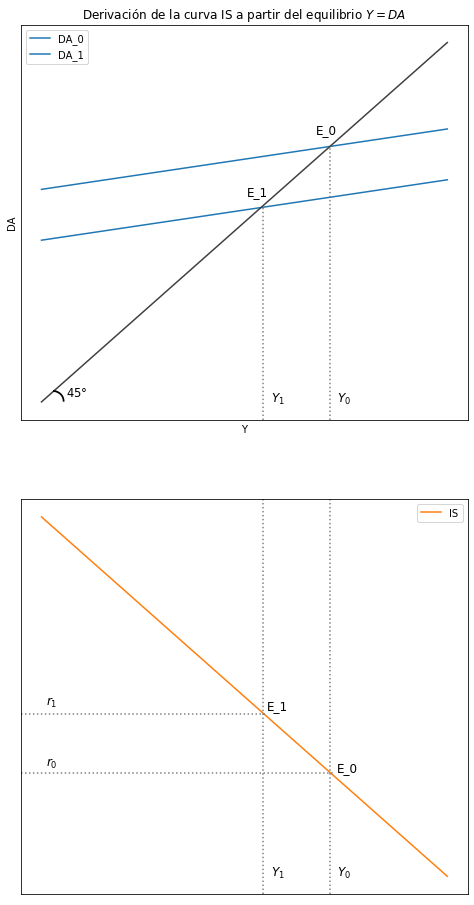
2.2. Derivación de la curva IS a partir de la Demanda Agregada#

Recordemos la ecuación del ingreso de equilibrio a corto plazo que fue obtenida a partir del equilibrio \((Y = DA)\):

\[ Y = \frac{1}{1 - (b - m)(1 - t)} (C_0 + I_0 + G_0 + X_0 - hr) \]

Esta ecuación, después de algunas operaciones, puede expresarse en función de la tasa de interés \((r)\):

\[ r = \frac{1}{h}(C_0 + G_0 + I_0 + X_0) - \frac{1 - (b - m)(1 - t)}{h}Y \]

Entonces, la curva IS puede ser simplificada de la siguiente manera:

\[ r = \frac{B_0}{h} - \frac{B_1}{h}Y \]

Donde \( B_0 = C_0 + G_0 + I_0 + X_0 \) y \( B_1 = 1 - (b - m)(1 - t) \)

Para la derivación gráfica, se tiene que recordar la ecuación de la Demanda Agregada \((DA)\):

Demanda Agregada:

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3
r = 0.9

Y = np.arange(Y_size)

# Ecuación de la curva del ingreso de equilibrio

def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
    DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
    return DA_K

DA_IS_K = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)

#--------------------------------------------------
# Recta de 45°

a = 2.5 

def L_45(a, Y):
    L_45 = a*Y
    return L_45

L_45 = L_45(a, Y)

#--------------------------------------------------
# Segunda curva de ingreso de equilibrio

    # Definir cualquier parámetro autónomo
Go = 35

# Generar la ecuación con el nuevo parámetro
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
    DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
    return DA_K

DA_G = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)

- Curva IS:

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

# Gráfico de la derivación de la curva IS a partir de la igualdad (DA = Y)

    # Dos gráficos en un solo cuadro (ax1 para el primero y ax2 para el segundo)
fig, (ax1, ax2) = plt.subplots(2, figsize=(8, 16)) 

#---------------------------------
    # Gráfico 1: ingreso de Equilibrio
ax1.yaxis.set_major_locator(plt.NullLocator())   
ax1.xaxis.set_major_locator(plt.NullLocator())

ax1.plot(Y, DA_IS_K, label = "DA_0", color = "C0") 
ax1.plot(Y, DA_G, label = "DA_1", color = "C0") 
ax1.plot(Y, L_45, color = "#404040") 

ax1.axvline(x = 70.5, ymin= 0, ymax = 0.69, linestyle = ":", color = "grey")
ax1.axvline(x = 54,  ymin= 0, ymax = 0.54, linestyle = ":", color = "grey")

ax1.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
ax1.text(2.5, -3, '$◝$', fontsize = 30, color = 'black')
ax1.text(72, 0, '$Y_0$', fontsize = 12, color = 'black')
ax1.text(56, 0, '$Y_1$', fontsize = 12, color = 'black')
ax1.text(67, 185, 'E_0', fontsize = 12, color = 'black')
ax1.text(50, 142, 'E_1', fontsize = 12, color = 'black')

ax1.set(title = "Derivación de la curva IS a partir del equilibrio $Y=DA$", xlabel = r'Y', ylabel = r'DA')
ax1.legend()

#---------------------------------
    # Gráfico 2: Curva IS

ax2.yaxis.set_major_locator(plt.NullLocator())   
ax2.xaxis.set_major_locator(plt.NullLocator())

ax2.plot(Y, r, label = "IS", color = "C1") 

ax2.axvline(x = 70.5, ymin= 0, ymax = 1, linestyle = ":", color = "grey")
ax2.axvline(x = 54,  ymin= 0, ymax = 1, linestyle = ":", color = "grey")
plt.axhline(y = 151.5, xmin= 0, xmax = 0.7, linestyle = ":", color = "grey")
plt.axhline(y = 165, xmin= 0, xmax = 0.55, linestyle = ":", color = "grey")

ax2.text(72, 128, '$Y_0$', fontsize = 12, color = 'black')
ax2.text(56, 128, '$Y_1$', fontsize = 12, color = 'black')
ax2.text(1, 153, '$r_0$', fontsize = 12, color = 'black')
ax2.text(1, 167, '$r_1$', fontsize = 12, color = 'black')
ax2.text(72, 152, 'E_0', fontsize = 12, color = 'black')
ax2.text(55, 166, 'E_1', fontsize = 12, color = 'black')

ax2.legend()

plt.show()

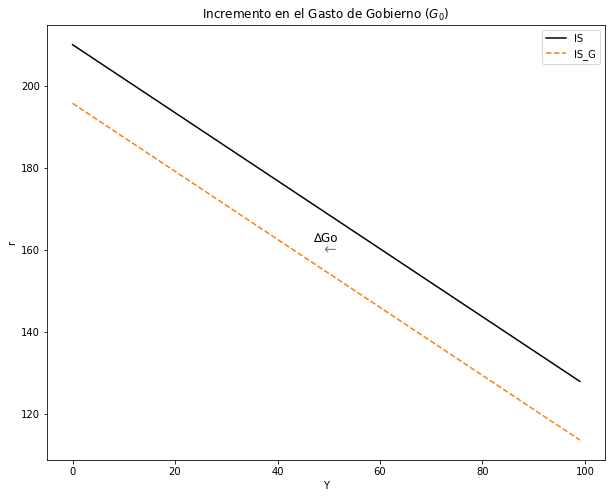
2.3. Estática comparativa en la curva IS#

2.3.1. Disminución en el Gasto de Gobierno \((G_0)\):#

#--------------------------------------------------
    # Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#--------------------------------------------------
    # NUEVA curva IS
    
# Definir SOLO el parámetro cambiado
Go = 60

# Generar la ecuación con el nuevo parámetro
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r_G = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

    # Gráfico

# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "black") #IS orginal
ax.plot(Y, r_G, label = "IS_G", color = "C1", linestyle = 'dashed') #Nueva IS

# Texto agregado
plt.text(47, 162, '∆Go', fontsize=12, color='black')
plt.text(49, 159, '←', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title = "Incremento en el Gasto de Gobierno $(G_0)$", xlabel= 'Y', ylabel= 'r')
ax.legend()

plt.show()

# Gráfico con movimiento

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3

Y = np.arange(Y_size)

def r_IS(b, m, t, Co, Io, Go, Xo, h, Y): # ecuación original
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r_G = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


    # Definir ecuación y gráfico para el parámetro específico
def r_IS_1(Go):
    r_IS_1 = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h  
    
    # gráfico
    plt.subplots(figsize=(10, 8))
    plt.plot(r_IS_1, label = "IS", color = "C1") # Curva IS orginal
    plt.plot(r_G, label = "IS_Go", color = "black") # Curva IS con movimiento
    plt.title('Gasto de Gobierno')
    plt.legend()    
    
    # crear gráfico con movimiento/control
Go_slide = widgets.FloatSlider(value = 70, min = 0, max = 110)  #widgets.FloatSlider(valor_inicial, min, max)
widgets.interact(r_IS_1, Go = Go_slide) #widgets.interact(nombre_función, parámetro = parámetro:_con_mov)

<function __main__.r_IS_1(Go)>

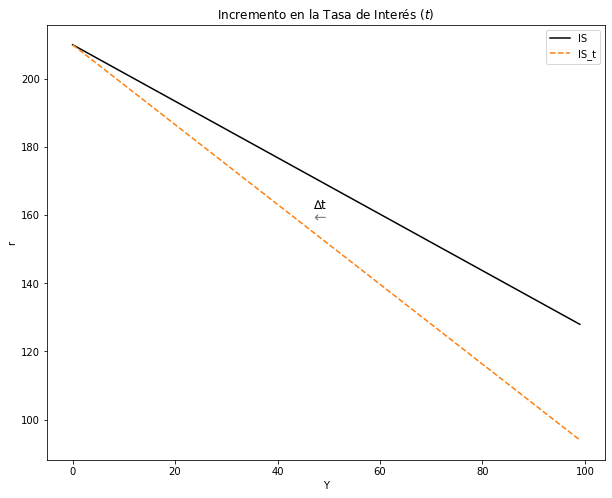
2.3.2. Incremento en la tasa impositiva \((t)\):#

#--------------------------------------------------
    # Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#--------------------------------------------------
    # NUEVA curva IS
    
# Definir SOLO el parámetro cambiado
t = 0.7

# Generar la ecuación con el nuevo parámetro
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r_t = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

    # Gráfico

# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "black") #IS orginal
ax.plot(Y, r_t, label = "IS_t", color = "C1", linestyle = 'dashed') #Nueva IS

# Texto agregado
plt.text(47, 162, '∆t', fontsize=12, color='black')
plt.text(47, 158, '←', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title = "Incremento en la Tasa de Interés $(t)$", xlabel= 'Y', ylabel= 'r')
ax.legend()

plt.show()

# Gráfico con movimiento

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3

Y = np.arange(Y_size)

def r_IS(b, m, t, Co, Io, Go, Xo, h, Y): # ecuación original
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r_t = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

    # Definir ecuación y gráfico para el parámetro específico
def r_IS_1(t):
    r_IS_1 = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h  
    
    # gráfico
    plt.subplots(figsize=(10, 8))
    plt.plot(r_IS_1, label = "IS", color = "C1") # Curva IS orginal
    plt.plot(r_t, label = "IS_t", color = "black") # Curva IS con movimiento
    plt.title('Tasa de Interés $(t)$')
    plt.legend()    
    
    # crear gráfico con movimiento/control
t_slide = widgets.FloatSlider(value = 0.3, min = 0, max = 1)  #widgets.FloatSlider(valor_inicial, min, max)
widgets.interact(r_IS_1, t = t_slide) #widgets.interact(nombre_función, parámetro = parámetro:_con_mov)

<function __main__.r_IS_1(t)>

2.4. Ejercicios#

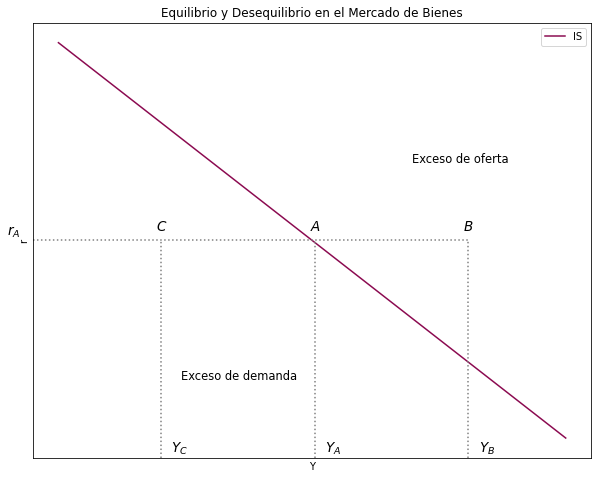
2.4.1. Grafique las áreas de exceso de oferta o exceso de demanda en el mercado de bienes. Explique por qué estos puntos están fuera de los puntos de equilibrio en el mercado de bienes#

Todos los puntos de la Curva IS corresponden a pares ordenados (Y, r) que equilibran el mercado de bienes. Por ejemplo, el punto \(A\) representa el equilibrio. Sin embargo, los puntos fuera de esta curva son de desequilibrio en el mercado o representan una situación en el que el ahorro y la inversión no son iguales.

Contrariamente el punto \(B\), que se encuentra a la derecha de la IS, representa un desequilibrio. Dado que la tasa de interés \((r)\) y la inversión \((I)\) permanecen constantes, pero los ingresos \((Y)\) son mayores, el ahorro de la gente es mayor que en el punto \(A\). Entonces, el ahorro es mayor a la inversión \((I < S)\) ; por lo tanto, \(AB\) a la derecha de la curva IS representa un exceso de oferta.

Asimismo, el punto \(C\), que se encuentra a la izquierda de la IS, representa un desequilibrio. Dado que la tasa de interés \((r)\) y la inversión \((I)\) permanecen constantes, pero el ingreso \((Y)\) es menor, el ahorro de la gente es menor que en el punto \(A\). Entonces, el ahorro es menor a la inversión \((S < I)\) ; por lo tanto, \(AC\) a la derecha de la curva IS representa un exceso de demanda.

# Gráfico de la curva IS

# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "#8B0A50") #Demanda agregada

plt.axvline(x=20,  ymin= 0, ymax= 0.5, linestyle = ":", color = "grey")
plt.axvline(x=50,  ymin= 0, ymax= 0.5, linestyle = ":", color = "grey")
plt.axvline(x=80,  ymin= 0, ymax= 0.5, linestyle = ":", color = "grey")

plt.axhline(y=169, xmin= 0, xmax= 0.78, linestyle = ":", color = "grey")

# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())   
ax.xaxis.set_major_locator(plt.NullLocator())

# Texto agregado
plt.text(-10, 170, '$r_A$', fontsize = 13.5, color = 'black')

plt.text(19, 171, '$C$', fontsize = 13.5, color = 'black')
plt.text(49, 171, '$A$', fontsize = 13.5, color = 'black')
plt.text(79, 171, '$B$', fontsize = 13.5, color = 'black')

plt.text(22, 125, '$Y_C$', fontsize = 13.5, color = 'black')
plt.text(52, 125, '$Y_A$', fontsize = 13.5, color = 'black')
plt.text(82, 125, '$Y_B$', fontsize = 13.5, color = 'black')

plt.text(24, 140, 'Exceso de demanda', fontsize = 11.5, color = 'black')
plt.text(69, 185, 'Exceso de oferta', fontsize = 11.5, color = 'black')

# Título, ejes y leyenda
ax.set(title = "Equilibrio y Desequilibrio en el Mercado de Bienes", xlabel= 'Y', ylabel= 'r')
ax.legend()

plt.show()

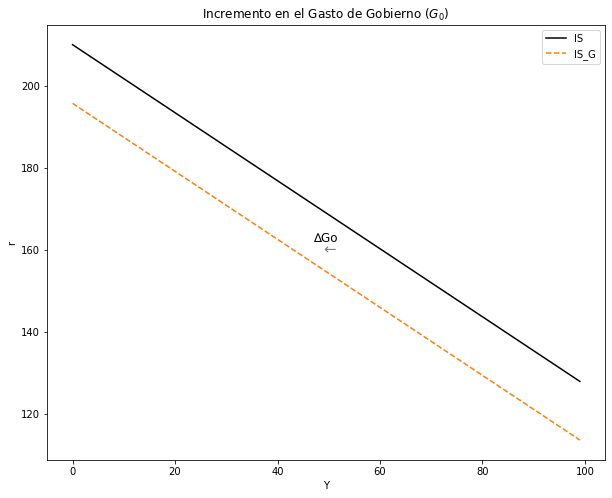
2.4.2. Analice una Política Fiscal Contractiva con caída del Gasto del Gobierno \((∆G_0 < 0)\).#

Intuición:

\[ ↓G_0 → DA↓ → DA < Y → Y↓ \]

Gráfico

#--------------------------------------------------
    # Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#--------------------------------------------------
    # NUEVA curva IS
    
# Definir SOLO el parámetro cambiado
Go = 60

# Generar la ecuación con el nuevo parámetro
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r_G = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

    # Gráfico

# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "black") #IS orginal
ax.plot(Y, r_G, label = "IS_G", color = "C1", linestyle = 'dashed') #Nueva IS

# Texto agregado
plt.text(47, 162, '∆Go', fontsize=12, color='black')
plt.text(49, 159, '←', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title = "Incremento en el Gasto de Gobierno $(G_0)$", xlabel= 'Y', ylabel= 'r')
ax.legend()

plt.show()

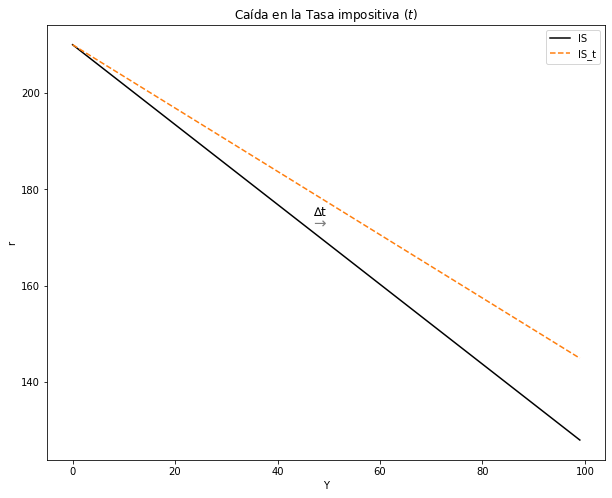
2.4.3. Analice una Política Fiscal Expansiva con una caída de la Tasa de Impuestos \((∆t < 0)\) .#

Intuición:

\[ ↓t → DA↑ → DA > Y → Y↑ \]

Gráfico

#--------------------------------------------------
    # Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo)/h - (Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#--------------------------------------------------
    # NUEVA curva IS
    
# Definir SOLO el parámetro cambiado
t = 0.1

# Generar la ecuación con el nuevo parámetro
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r_t = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

    # Gráfico

# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "black") #IS orginal
ax.plot(Y, r_t, label = "IS_t", color = "C1", linestyle = 'dashed') #Nueva IS

# Texto agregado
plt.text(47, 174.5, '∆t', fontsize=12, color='black')
plt.text(47, 172, '→', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title = "Caída en la Tasa impositiva $(t)$", xlabel= 'Y', ylabel= 'r')
ax.legend()

plt.show()

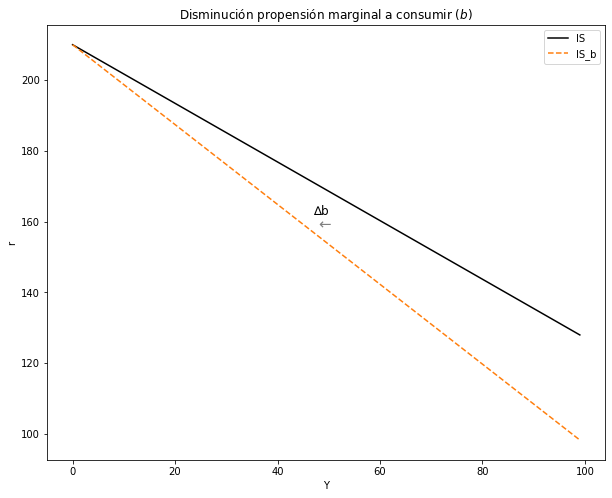
2.4.4. Analice una caída de la Propensión Marginal a Consumir \((∆b < 0)\).#

Intuición:

\[ ↓b → Co↓ → DA↓ → DA < Y → Y↓ \]

Gráfico

#--------------------------------------------------
    # Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#--------------------------------------------------
    # NUEVA curva IS
    
# Definir SOLO el parámetro cambiado
b = 0.5

# Generar la ecuación con el nuevo parámetro
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r_b = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

    # Gráfico

# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "black") #IS orginal
ax.plot(Y, r_b, label = "IS_b", color = "C1", linestyle = 'dashed') #Nueva IS

# Texto agregado
plt.text(47, 162, '∆b', fontsize=12, color='black')
plt.text(48, 158, '←', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title = "Disminución propensión marginal a consumir $(b)$", xlabel= 'Y', ylabel= 'r')
ax.legend()

plt.show()

Fundamentos de Macroeconomía

La curva IS (Inversión-Ahorro)

Contents