Mercado de Bienes: Consumo, Inversión, Determinación del Precio, y la Política Fiscal
Contents
import ipympl
%matplotlib widget
%matplotlib inline
import ipywidgets as widgets
import matplotlib.pyplot as plt
import matplotlib.widgets as widget
import numpy as np
import sympy as sy
from sympy import *
import pandas as pd
from causalgraphicalmodels import CausalGraphicalModel
import os
os.environ["PATH"] += os.pathsep + 'C:/Program Files/Graphviz/bin/'
from IPython.display import Image
import warnings
warnings.filterwarnings('ignore')
1. Mercado de Bienes: Consumo, Inversión, Determinación del Precio, y la Política Fiscal#
1.1. Modelo Keynesiano:#
Image('tutorial2.jpg')
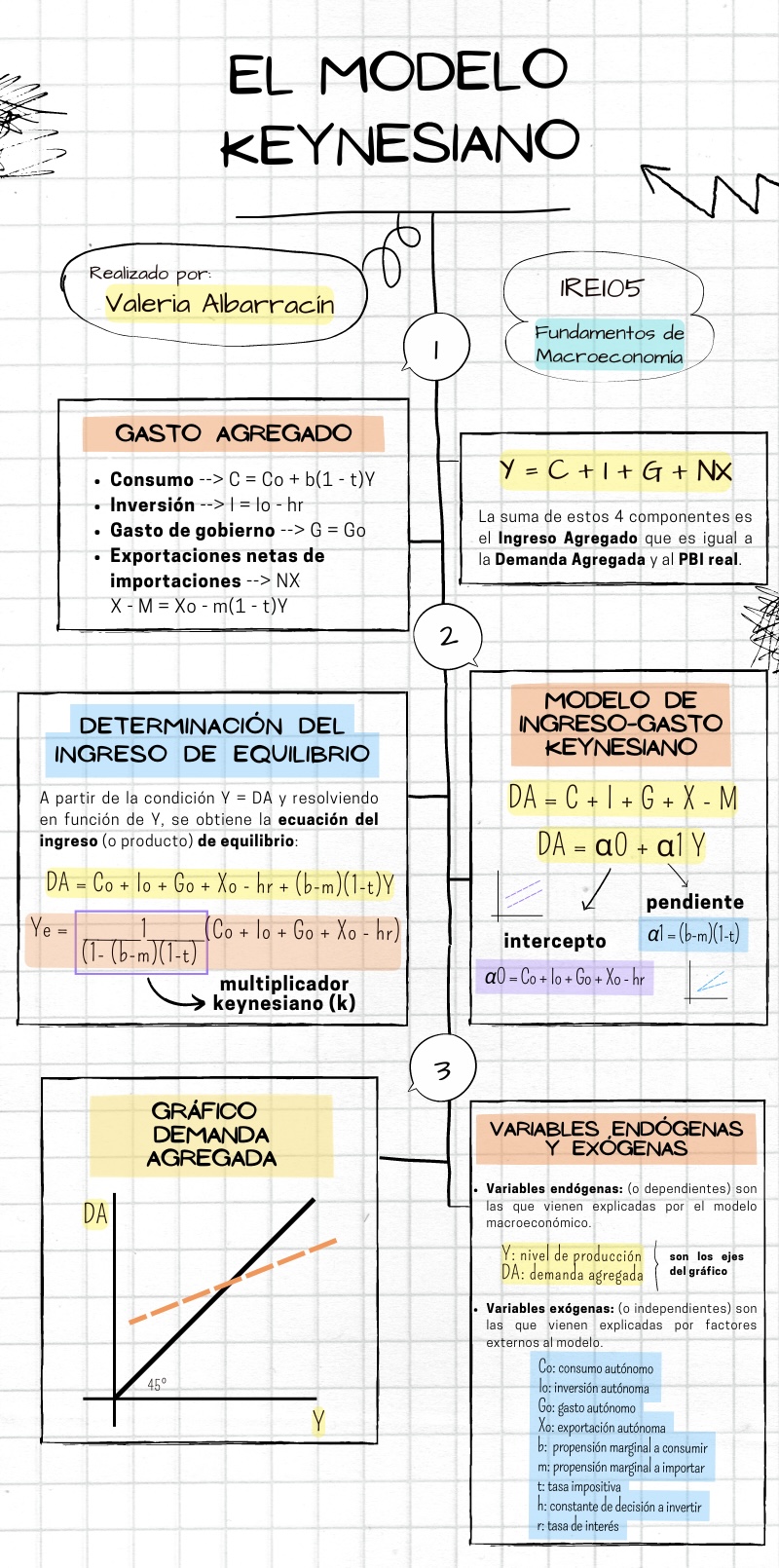
1.2. El modelo de Ingreso-Gasto Keynesiano:#
La ecuación de equilibrio para el Ingreso Agregado se deriva de la condición de equilibrio donde el ingreso es igual a la demanda agregada: \(DA = Y\):
\[ DA = C + I + G + X - M \]
Donde:
\[ C = C_0 + bY^d \]
\[ I = I_0 - hr \]
\[ G = G_0 \]
\[ X = X_0 \]
\[ M = mY^d \]
\[ Y^d = 1 - t \]
Entonces:
\[ DA = C_0 + I_0 + G_0 + X_0 - hr + Y(b - m)(1 - t) \]
De forma corta:
\[ DA = α_0 + α_1Y \]
Donde \( α_0 = (C_0 + I_0 + G_0 + X_0 -hr)\) es el intercepto y \( α_1 = (b - m)(1 - t) \) es la pendiente de la función
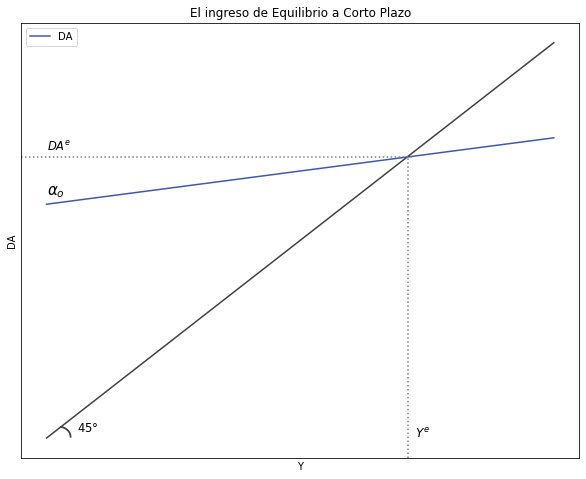
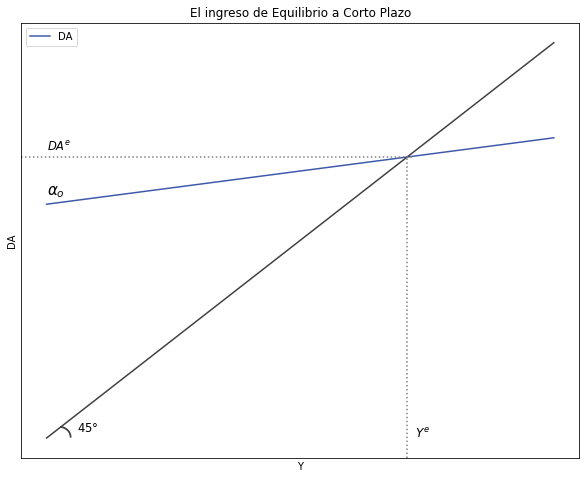
Ahora, considerando la condición de equilibrio \(Y = DA\), la ecuación del ingreso de equilibrio a corto plazo es:
\[ Y = C_0 + bY^d + I_0 -hr + G_0 + X_0 - mY^d \]
\[ Y = \frac{1}{1 - (b - m)(1 - t)} (C_0 + I_0 + G_0 + X_0 - hr) \]
El ingreso de Equilibrio a corto plazo se grafica de la siguiente forma:
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8 # b > m
m = 0.2
t = 0.3
r = 0.9
Y = np.arange(Y_size)
# Ecuación de la curva del ingreso de equilibrio
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_IS_K = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
# Recta de 45°
a = 2.5
def L_45(a, Y):
L_45 = a*Y
return L_45
L_45 = L_45(a, Y)
# Gráfico
# Dimensiones del gráfico
y_max = np.max(DA_IS_K)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(DA_IS_K, label = "DA", color = "#3D59AB") #Demanda agregada
ax.plot(L_45, color = "#404040") #Línea de 45º
# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_locator(plt.NullLocator())
# Líneas punteadas punto de equilibrio
plt.axvline(x=70.5, ymin= 0, ymax= 0.69, linestyle = ":", color = "grey")
plt.axhline(y=176, xmin= 0, xmax= 0.7, linestyle = ":", color = "grey")
# Texto agregado
# punto de equilibrio
plt.text(0, 180, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(72, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(0, 152, '$α_o$', fontsize = 15, color = 'black')
# línea 45º
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
# Título y leyenda
ax.set(title="El ingreso de Equilibrio a Corto Plazo", xlabel= r'Y', ylabel= r'DA')
ax.legend() #mostrar leyenda
plt.show()
# líneas punteadas autómaticas
# definir la función line_intersection
def line_intersection(line1, line2):
xdiff = (line1[0][0] - line1[1][0], line2[0][0] - line2[1][0])
ydiff = (line1[0][1] - line1[1][1], line2[0][1] - line2[1][1])
def det(a, b):
return a[0] * b[1] - a[1] * b[0]
div = det(xdiff, ydiff)
if div == 0:
raise Exception('lines do not intersect')
d = (det(*line1), det(*line2))
x = det(d, xdiff) / div
y = det(d, ydiff) / div
return x, y
# coordenadas de las curvas (x,y)
A = [DA_IS_K[0], Y[0]] # DA, coordenada inicio
B = [DA_IS_K[-1], Y[-1]] # DA, coordenada fin
C = [L_45[0], Y[0]] # L_45, coordenada inicio
D = [L_45[-1], Y[-1]] # L_45, coordenada fin
# creación de intersección
intersec = line_intersection((A, B), (C, D))
intersec # (y,x)
(175.9254807692308, 70.37019230769232)
# Gráfico
# Dimensiones del gráfico
y_max = np.max(DA_IS_K)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, DA_IS_K, label = "DA", color = "#3D59AB") #Demanda agregada
ax.plot(Y, L_45, color = "#404040") #Línea de 45º
# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_locator(plt.NullLocator())
# Líneas punteadas punto de equilibrio
plt.axhline(y=intersec[0], xmin= 0, xmax= 0.7, linestyle = ":", color = "grey")
plt.axvline(x=intersec[1], ymin= 0, ymax= 0.69, linestyle = ":", color = "grey")
# Texto agregado
# punto de equilibrio
plt.text(0, 180, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(72, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(0, 152, '$α_o$', fontsize = 15, color = 'black')
# línea 45º
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
# Título y leyenda
ax.set(title="El ingreso de Equilibrio a Corto Plazo", xlabel= r'Y', ylabel= r'DA')
ax.legend() #mostrar leyenda
plt.show()
1.2.1. Estática comparativa del modelo de Ingreso-Gasto Keynesiano:#
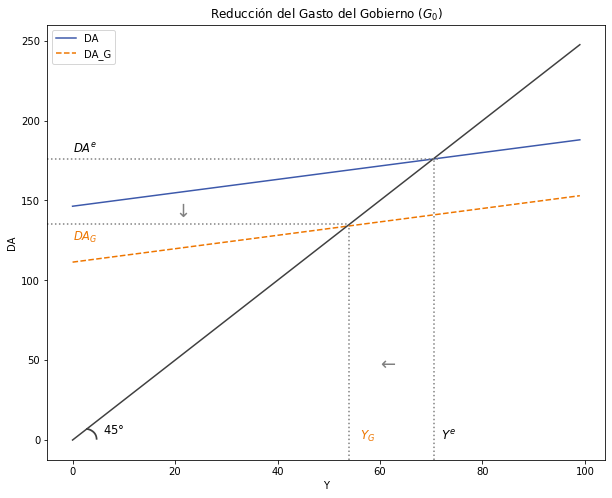
1.2.1.1. Política Fiscal contractiva con reducción del Gasto del Gobierno \((G_0)\):#
#--------------------------------------------------
# Curva de ingreso de equilibrio ORIGINAL
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3
r = 0.9
Y = np.arange(Y_size)
# Ecuación
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_IS_K = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
#--------------------------------------------------
# NUEVA curva de ingreso de equilibrio
# Definir SOLO el parámetro cambiado
Go = 35
# Generar la ecuación con el nuevo parámetro
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_G = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
# Gráfico
y_max = np.max(DA_IS_K)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, DA_IS_K, label = "DA", color = "#3D59AB") #curva ORIGINAL
ax.plot(Y, DA_G, label = "DA_G", color = "#EE7600", linestyle = 'dashed') #NUEVA curva
ax.plot(Y, L_45, color = "#404040") #línea de 45º
# Lineas punteadas
plt.axvline(x = 70.5, ymin= 0, ymax = 0.69, linestyle = ":", color = "grey")
plt.axhline(y = 176, xmin= 0, xmax = 0.7, linestyle = ":", color = "grey")
plt.axvline(x = 54, ymin= 0, ymax = 0.54, linestyle = ":", color = "grey")
plt.axhline(y = 135, xmin= 0, xmax = 0.54, linestyle = ":", color = "grey")
# Texto agregado
plt.text(0, 180, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(0, 125, '$DA_G$', fontsize = 11.5, color = '#EE7600')
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
plt.text(72, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(56, 0, '$Y_G$', fontsize = 12, color = '#EE7600')
plt.text(60, 45, '$←$', fontsize = 18, color = 'grey')
plt.text(20, 140, '$↓$', fontsize = 18, color = 'grey')
# Título y leyenda
ax.set(title = "Reducción del Gasto del Gobierno $(G_0)$", xlabel = r'Y', ylabel = r'DA')
ax.legend()
plt.show()
# Gráfico con movimiento
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3
r = 0.9
Y = np.arange(Y_size)
# Definir ecuación y gráfico para el parámetro específico
def DA_K(Go): # ecuación
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
# gráfico
plt.subplots(figsize=(10, 8))
plt.plot(Y, DA_K, label = "DA", color = "#3D59AB") #Demanda agregada
plt.plot(Y, L_45, color = "#404040")
plt.title('Gasto de Gobierno')
plt.legend()
# crear gráfico con movimiento/control
Go_slide = widgets.FloatSlider(value = 70, min = 0, max = 110) #widgets.FloatSlider(valor_inicial, min, max)
widgets.interact(DA_K, Go = Go_slide) #widgets.interact(nombre_función, parámetro = parámetro:_con_mov)
<function __main__.DA_K(Go)>
Intuición:
\[ ↓Go → ↓DA → DA < Y → ↓Y \]
# Gráfico de causalidad
sprinkler = CausalGraphicalModel(nodes=["Go ↓","DA ↓","Y ↓"],
edges=[("Go ↓","DA ↓"), ("DA ↓","Y ↓")])
sprinkler.draw()
Matemáticamente: \(∆G_0 < 0 → ¿∆Y?\)
\[ Y = \frac{1}{1 - (b - m)(1 - t)} (C_0 + I_0 + G_0 + X_0 - hr) \]
o, considerando el multiplicador keynesiano, \( k > 0 \):
\[ Y = k (C_0 + I_0 + G_0 + X_0 - hr) \]
\[ ∆Y = k (∆C_0 + ∆I_0 + ∆G_0 + ∆X_0 - ∆hr) \]
Pero, si no ha habido cambios en \(C_0\), \(I_0\), \(X_0\), \(h\) ni \(r\), entonces:
\[∆C_0 = ∆I_0 = ∆X_0 = ∆h = ∆r = 0\]
\[ ∆Y = k (∆G_0) \]
Sabiendo que \(∆G_0 < 0 \) y que \(k > 0\), la multiplicación de un número negativo con un positivo dará otro negativo:
\[ ∆Y = (+)(-) \]
\[ ∆Y < 0 \]
# Diferenciales
# nombrar variables como símbolos
Co, Io, Go, Xo, h, r, b, m, t = symbols('Co Io Go Xo h r b m t')
# determinar ecuación
f = (Co + Io + Go + Xo - h*r)/(1-(b-m)*(1-t))
# función diferencial
df_Go = diff(f, Go) # diff(función, variable_analizar
df_Go #∆Y/∆Go
\[\displaystyle \frac{1}{- \left(1 - t\right) \left(b - m\right) + 1}\]
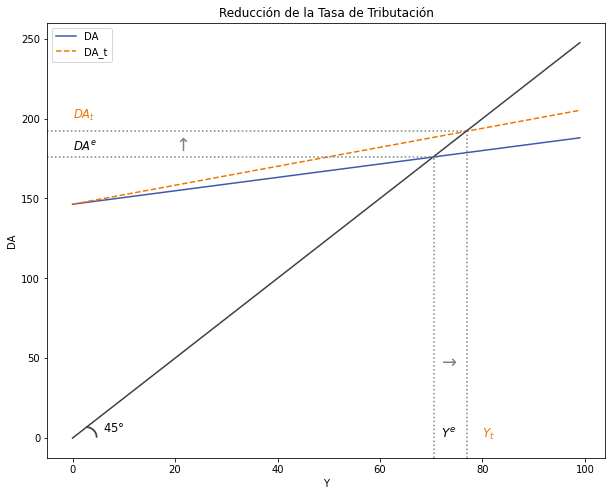
1.2.1.2. Política fiscal expansiva con una reducción de la Tasa de Tributación \((t)\):#
#--------------------------------------------------
# Curva de ingreso de equilibrio ORIGINAL
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3 #tasa de tributación
r = 0.9
Y = np.arange(Y_size)
# Ecuación
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_IS_K = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
#--------------------------------------------------
# NUEVA curva de ingreso de equilibrio
# Definir SOLO el parámetro cambiado
t = 0.01
# Generar la ecuación con el nuevo parámetros
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_t = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
# Gráfico
y_max = np.max(DA_IS_K)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, DA_IS_K, label = "DA", color = "#3D59AB") #curva ORIGINAL
ax.plot(Y, DA_t, label = "DA_t", color = "#EE7600", linestyle = 'dashed') #NUEVA curva
ax.plot(Y, L_45, color = "#404040") #línea de 45º
# Lineas punteadas
plt.axvline(x = 70.5, ymin= 0, ymax = 0.69, linestyle = ":", color = "grey")
plt.axhline(y = 176, xmin= 0, xmax = 0.7, linestyle = ":", color = "grey")
plt.axvline(x = 77, ymin= 0, ymax = 0.75, linestyle = ":", color = "grey")
plt.axhline(y = 192, xmin= 0, xmax = 0.75, linestyle = ":", color = "grey")
# Texto agregado
plt.text(0, 180, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(0, 200, '$DA_t$', fontsize = 11.5, color = '#EE7600')
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
plt.text(72, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(80, 0, '$Y_t$', fontsize = 12, color = '#EE7600')
plt.text(72, 45, '$→$', fontsize = 18, color = 'grey')
plt.text(20, 180, '$↑$', fontsize = 18, color = 'grey')
# Título y leyenda
ax.set(title = "Reducción de la Tasa de Tributación", xlabel = r'Y', ylabel = r'DA')
ax.legend()
plt.show()
# Gráfico con movimiento
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3
r = 0.9
Y = np.arange(Y_size)
# Definir ecuación y gráfico para el parámetro específico
def DA_K(t): # ecuación
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
# gráfico
plt.subplots(figsize=(10, 8))
plt.plot(Y, DA_K, label = "DA", color = "#3D59AB") #Demanda agregada
plt.plot(Y, L_45, color = "#404040")
plt.title('Tasa de Tributación')
plt.legend()
# crear gráfico con movimiento/control
t_slide = widgets.FloatSlider(value = 0.5, min = 0, max = 3) #widgets.FloatSlider(valor_inicial, min, max)
widgets.interact(DA_K, t = t_slide) #widgets.interact(nombre_función, parámetro = parámetro:_con_mov)
<function __main__.DA_K(t)>
Intuición: ¿contradicción?
\[ t↓ → Co↑ → DA↑ → DA > Y → Y↑ \]
\[ t↓ → M↑ → DA↓ → DA < Y → Y↓ \]
Matemáticamente: \(∆t < 0 → ¿∆Y?\)
Co, Io, Go, Xo, h, r, b, m, t = symbols('Co Io Go Xo h r b m t')
f = (Co + Io + Go + Xo - h*r)/(1-(b-m)*(1-t))
df_t = diff(f, t)
df_t #∆Y/∆t
\[\displaystyle \frac{\left(- b + m\right) \left(Co + Go + Io + Xo - h r\right)}{\left(- \left(1 - t\right) \left(b - m\right) + 1\right)^{2}}\]
Considernado el diferencial de \(∆t\):
\[ \frac{∆Y}{∆t} = \frac{(m-b)(Co + Go + Io + Xo - hr)}{(1-(1-t)(b-m)+1)^2} \]
Sabiendo que b > m, entonces \((m-b) < 0\)
Los componentes autónomos no cambian: \(∆C_0 = ∆I_0 = ∆X_0 = ∆h = ∆r = 0\)
Cualquier número elevado al cuadrado será positivo: \( (1-(1-t)(b-m)+1)^2 > 0 \)
Entonces:
\[ \frac{∆Y}{∆t} = \frac{(-)}{(+)} \]
Dado que \(∆t < 0\), la división de dos positivos da otro positivo:
\[ \frac{∆Y}{(-)} = \frac{(-)}{(+)} \]
\[ ∆Y = \frac{(-)(-)}{(+)} \]
\[ ∆Y > 0 \]
1.3. Ejercicios:#
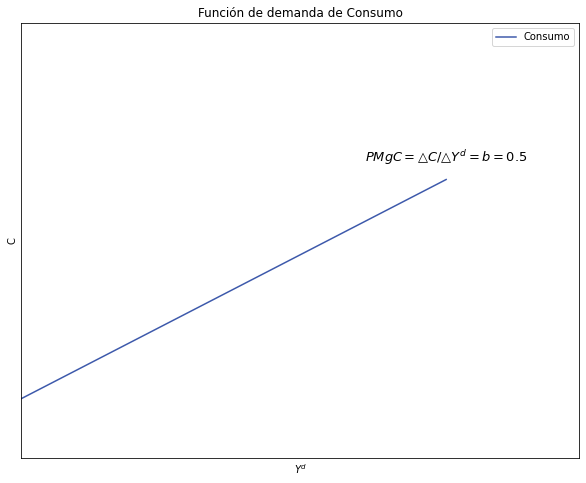
1.3.1. Derive y grafique la función de demanda de Consumo.#
# Parámetros
Y_size = 100
Co = 35
b = 0.8
t = 0.3
Y = np.arange(Y_size)
# Ecuación de la curva del ingreso de equilibrio
def C(Co, b, t, Y):
C = Co + b*(1-t)*Y
return C
C = C(Co, b, t, Y)
# Gráfico
# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))
custom_xlim = (0, 130)
custom_ylim = (20, 130)
plt.setp(ax, xlim=custom_xlim, ylim=custom_ylim)
# Curvas a graficar
ax.plot(Y, C, label = "Consumo", color = "#3D59AB") #Demanda agregada
# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_locator(plt.NullLocator())
# Texto agregado
# punto de equilibrio
plt.text(80, 95, '$PMgC = △C/△Y^d = b = 0.5$', fontsize = 13, color = 'black')
# Título y leyenda
ax.set(title="Función de demanda de Consumo", xlabel= '$Y^d$', ylabel= 'C')
ax.legend() #mostrar leyenda
plt.show()
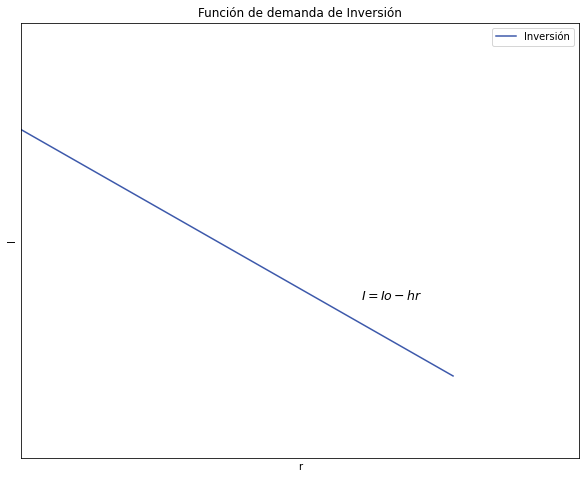
1.3.2. Derive y grafique la función de demanda de Inversión.#
# Parámetros
Io = 40
h = 0.7
r = np.arange(start = 0.01, stop = 1, step =0.01)
r
# Ecuación de la curva del ingreso de equilibrio
def I(Io, h, r):
I = Io - h*r
return I
I = I(Io, h, r)
# Gráfico
# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))
custom_xlim = (0.1, 1.25)
custom_ylim = (39.1, 40.2)
plt.setp(ax, xlim=custom_xlim, ylim=custom_ylim)
# Curvas a graficar
ax.plot(r, I, label = "Inversión", color = "#3D59AB") #Demanda agregada
# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_locator(plt.NullLocator())
# Texto agregado
# punto de equilibrio
plt.text(0.8, 39.5, '$I = Io - hr$', fontsize = 12.5, color = 'black')
# Título y leyenda
ax.set(title="Función de demanda de Inversión", xlabel= 'r', ylabel= 'I')
ax.legend() #mostrar leyenda
plt.show()
1.3.3. ¿Cuáles son los supuestos del modelo Ingreso-Gasto Keynesiano?#
Es un modelo de corto plazo.
El nivel de precios es rígido o fijo.
El nivel del producción \((Y)\) se adapta a los cambios de la Demanda Agregada \((DA)\).
La tasa de interés \((r)\) se determina afuera del modelo de Ingreso-Gasto. Se da en el mercado monetario \((LM)\).
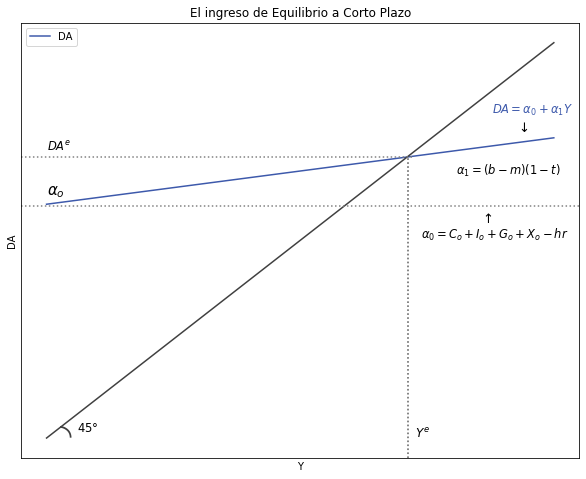
1.3.4. Encuentre y grafique el nivel de Ingreso de equilibrio \(Y^e\) del modelo Ingreso-Gasto Keynesiano:#
La ecuación de equilibrio para el Ingreso se deriva de la condición de equilibrio donde el nivel de producción es igual a la Demanda Agregada: \(DA = Y\):
\[ DA = C + I + G + X - M \]
Donde:
\[ C = C_0 + bY^d \]
\[ I = I_0 - hr \]
\[ G = G_0 \]
\[ X = X_0 \]
\[ M = mY^d \]
\[ Y^d = 1 - t \]
Entonces:
\[ DA = C_0 + I_0 + G_0 + X_0 - hr + Y(b - m)(1 - t) \]
De forma corta:
\[ DA = α_0 + α_1Y \]
Donde \( α_0 = (C_0 + I_0 + G_0 + X_0 -hr)\) es el intercepto y \( α_1 = (b - m)(1 - t) \) es la pendiente de la función
Ahora, considerando la condición de equilibrio \(Y = DA\), la ecuación del ingreso de equilibrio a corto plazo es:
\[ Y^e = C_0 + bY^d + I_0 -hr + G_0 + X_0 - mY^d \]
\[ Y^e = \frac{1}{1 - (b - m)(1 - t)} (C_0 + I_0 + G_0 + X_0 - hr) \]
Donde \(\frac{1}{1 - (b - m)(1 - t)}\) es el multiplicador keynesiano \((k)\).
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8 # b > m
m = 0.2
t = 0.3
r = 0.9
Y = np.arange(Y_size)
# Ecuación de la curva del ingreso de equilibrio
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_IS_K = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
# Recta de 45°
a = 2.5
def L_45(a, Y):
L_45 = a*Y
return L_45
L_45 = L_45(a, Y)
# Gráfico
# Dimensiones del gráfico
y_max = np.max(DA_IS_K)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(DA_IS_K, label = "DA", color = "#3D59AB") #Demanda agregada
ax.plot(L_45, color = "#404040") #Línea de 45º
# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_locator(plt.NullLocator())
# Líneas punteadas punto de equilibrio
plt.axvline(x=70.5, ymin= 0, ymax= 0.69, linestyle = ":", color = "grey")
plt.axhline(y=176, xmin= 0, xmax= 0.7, linestyle = ":", color = "grey")
plt.axvline(x=70.5, ymin= 0, ymax= 0.69, linestyle = ":", color = "grey")
plt.axhline(y=145, xmin= 0, xmax= 1, linestyle = ":", color = "grey")
# Texto agregado
# punto de equilibrio
plt.text(0, 180, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(72, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(0, 152, '$α_o$', fontsize = 15, color = 'black')
# línea 45º
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
# ecuaciones
plt.text(87, 203, '$DA = α_0 + α_1 Y$', fontsize = 11.5, color = '#3D59AB')
plt.text(80, 165, '$α_1 = (b-m)(1-t)$', fontsize = 11.5, color = 'black')
plt.text(73, 125, '$α_0 = C_o + I_o + G_o + X_o - hr$', fontsize = 11.5, color = 'black')
plt.text(92, 192, '$↓$', fontsize = 13, color = 'black')
plt.text(85, 135, '$↑$', fontsize = 13, color = 'black')
# Título y leyenda
ax.set(title="El ingreso de Equilibrio a Corto Plazo", xlabel= r'Y', ylabel= r'DA')
ax.legend() #mostrar leyenda
plt.show()
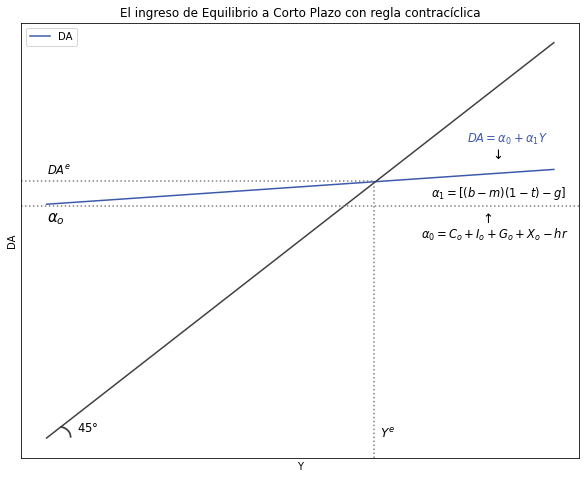
1.3.5. El modelo de Ingreso-Gasto keynesiano con Regla Contracíclica:#
1.3.5.1. Grafique la Funcion de demanda Agregada y la recta de 45 grados señalando los valores de intercepto y pendiente#
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
g = 0.2 #solo valores entre 0-0.4
Xo = 2
h = 0.7
b = 0.8 # b > m
m = 0.2
t = 0.3
r = 0.9
Y = np.arange(Y_size)
# Ecuación de la curva del ingreso de equilibrio
def DA_C(Co, Io, Go, Xo, h, r, b, m, t, g, Y):
DA_C = (Co + Io + Go + Xo - h*r) + [(b-m)*(1-t)-g]*Y
return DA_C
DA_Cont = DA_C(Co, Io, Go, Xo, h, r, b, m, t, g, Y)
# Gráfico
# Dimensiones del gráfico
y_max = np.max(DA_Cont)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(DA_Cont, label = "DA", color = "#3D59AB") #Demanda agregada
ax.plot(L_45, color = "#404040") #Línea de 45º
# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_locator(plt.NullLocator())
# Líneas punteadas punto de equilibrio
plt.axvline(x=64, ymin= 0, ymax= 0.63, linestyle = ":", color = "grey")
plt.axhline(y=161, xmin= 0, xmax= 0.63, linestyle = ":", color = "grey")
plt.axhline(y=145, xmin= 0, xmax= 1, linestyle = ":", color = "grey")
# Texto agregado
# punto de equilibrio
plt.text(0, 165, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(65, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(0, 135, '$α_o$', fontsize = 15, color = 'black')
# línea 45º
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
# ecuaciones
plt.text(82, 185, '$DA = α_0 + α_1 Y$', fontsize = 11.5, color = '#3D59AB')
plt.text(75, 151, '$α_1 = [(b-m)(1-t)-g]$', fontsize = 11.5, color = 'black')
plt.text(73, 125, '$α_0 = C_o + I_o + G_o + X_o - hr$', fontsize = 11.5, color = 'black')
plt.text(87, 175, '$↓$', fontsize = 13, color = 'black')
plt.text(85, 135, '$↑$', fontsize = 13, color = 'black')
# Título y leyenda
ax.set(title="El ingreso de Equilibrio a Corto Plazo con regla contracíclica", xlabel= r'Y', ylabel= r'DA')
ax.legend() #mostrar leyenda
plt.show()
1.3.5.2. Encuentre el nivel de Ingreso de Equilibrio#
La ecuación de equilibrio para el Ingreso se deriva de la condición de equilibrio donde el nivel de producción es igual a la Demanda Agregada: \(DA = Y\):
\[ DA = C + I + G + X - M \]
Donde:
\[ C = C_0 + bY^d \]
\[ I = I_0 - hr \]
\[ G = G_0 - gY \]
\[ X = X_0 \]
\[ M = mY^d \]
\[ Y^d = 1 - t \]
Entonces:
\[ DA = C_0 + I_0 + G_0 + X_0 - hr + Y[(b - m)(1 - t) - g] \]
De forma corta:
\[ DA = α_0 + α_1Y \]
Donde \( α_0 = (C_0 + I_0 + G_0 + X_0 -hr)\) es el intercepto y \( α_1 = [(b - m)(1 - t) - g] \) es la pendiente de la función
Ahora, considerando la condición de equilibrio \(Y = DA\), la ecuación del ingreso de equilibrio a corto plazo es:
\[ Y^e = \frac{1}{1 - (b - m)(1 - t) + g} (C_0 + I_0 + G_0 + X_0 - hr) \]
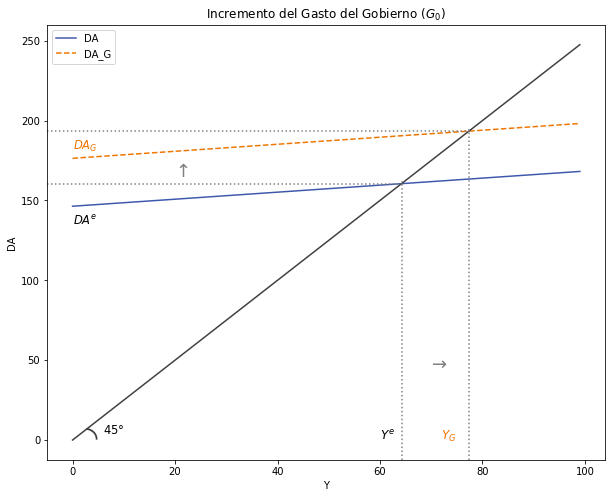
1.3.5.3. Analice una Política Fiscal Expansiva con aumento del Gasto del Gobierno#
Intuición:
\[ ↑Go → ↑DA → DA > Y → ↑Y \]
Matemáticamente: \(∆G_0 < 0 → ¿∆Y?\)
# Diferenciales
# nombrar variables como símbolos
Co, Io, Go, Xo, h, r, b, m, t, g = symbols('Co Io Go Xo h r b m t g')
# determinar ecuación
f = (Co + Io + Go + Xo - h*r)/(1 - (b - m)*(1 - t) + g)
# función diferencial
df_Go = diff(f, Go) # diff(función, variable_analizar
df_Go #∆Y/∆Go
\[\displaystyle \frac{1}{g - \left(1 - t\right) \left(b - m\right) + 1}\]
Considernado el diferencial obtenido:
\[ \frac{∆Y}{∆Go} = \frac{1}{1 - (b - m)(1 - t) + g} \]
Sabiendo que al multiplicador keynesiano \((k > 0)\) se le adiciona el parámetro \(g\), el denominador continuará siendo positivo (aunque más grande y con una pendiente de curva reducida).
Y considerando que \(∆G_0 > 0 \), la multiplicación de un número positivo con otro positivo dará un positivo:
\[ \frac{∆Y}{(+)} = (+) \]
\[ ∆Y = (+)(+) \]
\[ ∆Y > 0 \]
Gráficamente:
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3
r = 0.9
g = 0.2
Y = np.arange(Y_size)
# Ecuación de la curva del ingreso de equilibrio
def DA_C(Co, Io, Go, Xo, h, r, b, m, t, g, Y):
DA_C = (Co + Io + Go + Xo - h*r) + [(b-m)*(1-t)-g]*Y
return DA_C
DA_Cont = DA_C(Co, Io, Go, Xo, h, r, b, m, t, g, Y)
# Nueva curva
Go = 100
def DA_C(Co, Io, Go, Xo, h, r, b, m, t, g, Y):
DA_C = (Co + Io + Go + Xo - h*r) + [(b-m)*(1-t)-g]*Y
return DA_C
DA_C_G = DA_C(Co, Io, Go, Xo, h, r, b, m, t, g, Y)
# líneas punteadas autómaticas
# definir la función line_intersection
def line_intersection(line1, line2):
xdiff = (line1[0][0] - line1[1][0], line2[0][0] - line2[1][0])
ydiff = (line1[0][1] - line1[1][1], line2[0][1] - line2[1][1])
def det(a, b):
return a[0] * b[1] - a[1] * b[0]
div = det(xdiff, ydiff)
if div == 0:
raise Exception('lines do not intersect')
d = (det(*line1), det(*line2))
x = det(d, xdiff) / div
y = det(d, ydiff) / div
return x, y
# coordenadas de las curvas (x,y)
A = [DA_Cont[0], Y[0]] # DA, coordenada inicio
B = [DA_Cont[-1], Y[-1]] # DA, coordenada fin
C = [L_45[0], Y[0]] # L_45, coordenada inicio
D = [L_45[-1], Y[-1]] # L_45, coordenada fin
# creación de intersección
intersec = line_intersection((A, B), (C, D))
intersec # (y,x)
(160.4934210526316, 64.19736842105264)
# coordenadas de las curvas (x,y)
A = [DA_C_G[0], Y[0]] # DA, coordenada inicio
B = [DA_C_G[-1], Y[-1]] # DA, coordenada fin
C = [L_45[0], Y[0]] # L_45, coordenada inicio
D = [L_45[-1], Y[-1]] # L_45, coordenada fin
# creación de intersección
intersec_G = line_intersection((A, B), (C, D))
intersec_G # (y,x)
(193.38815789473685, 77.35526315789474)
# Gráfico
y_max = np.max(DA_Cont)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(DA_Cont, label = "DA", color = "#3D59AB") #curva ORIGINAL
ax.plot(DA_C_G, label = "DA_G", color = "#EE7600", linestyle = 'dashed') #NUEVA curva
ax.plot(L_45, color = "#404040") #línea de 45º
# Lineas punteadas
plt.axhline(y=intersec[0], xmin= 0, xmax= 0.64, linestyle = ":", color = "grey")
plt.axvline(x=intersec[1], ymin= 0, ymax= 0.64, linestyle = ":", color = "grey")
plt.axhline(y=intersec_G[0], xmin= 0, xmax= 0.76, linestyle = ":", color = "grey")
plt.axvline(x=intersec_G[1], ymin= 0, ymax= 0.76, linestyle = ":", color = "grey")
# Texto agregado
plt.text(0, 135, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(0, 182, '$DA_G$', fontsize = 11.5, color = '#EE7600')
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
plt.text(60, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(72, 0, '$Y_G$', fontsize = 12, color = '#EE7600')
plt.text(70, 45, '$→$', fontsize = 18, color = 'grey')
plt.text(20, 165, '$↑$', fontsize = 18, color = 'grey')
# Título y leyenda
ax.set(title = "Incremento del Gasto del Gobierno $(G_0)$", xlabel = r'Y', ylabel = r'DA')
ax.legend()
plt.show()
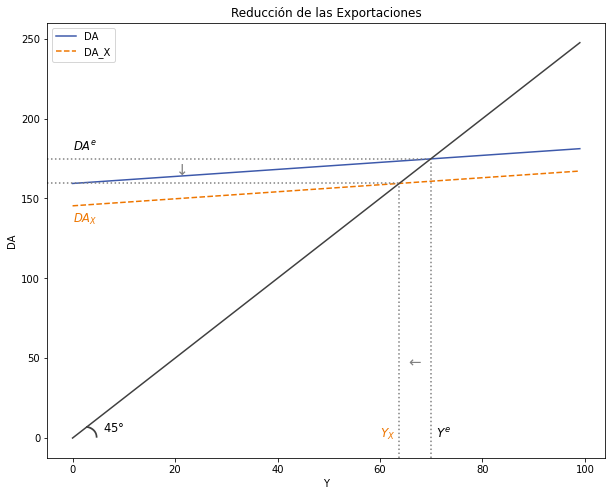
1.3.5.4. Analice una crisis mundial que reduce nuestras exportaciones \((M<0)\).#
Intuición:
\[ ↓Xo → ↓DA → DA < Y → ↓Y \]
Matemáticamente:
# Diferenciales
# nombrar variables como símbolos
Co, Io, Go, Xo, h, r, b, m, t, g = symbols('Co Io Go Xo h r b m t g')
# determinar ecuación
f = (Co + Io + Go + Xo - h*r)/(1 - (b - m)*(1 - t) + g)
# función diferencial
df_Xo = diff(f, Xo) # diff(función, variable_analizar
df_Xo #∆Y/∆Go
\[\displaystyle \frac{1}{g - \left(1 - t\right) \left(b - m\right) + 1}\]
Considernado el diferencial obtenido:
\[ \frac{∆Y}{∆X_0} = \frac{1}{1 - (b - m)(1 - t) + g} \]
Sabiendo que al multiplicador keynesiano \((k > 0)\) se le adiciona el parámetro \(g\), el denominador continuará siendo positivo (aunque más grande y con una pendiente de curva reducida).
Y considerando que \(∆X_0 < 0 \), la multiplicación de un número positivo con un negativo dará un negativo:
\[ \frac{∆Y}{(-)} = (+) \]
\[ ∆Y = (-)(+) \]
\[ ∆Y < 0 \]
Gráficamente
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
g = 0.2 #solo valores entre 0-0.4
Xo = 15
h = 0.7
b = 0.8 # b > m
m = 0.2
t = 0.3
r = 0.9
Y = np.arange(Y_size)
# Ecuación de la curva del ingreso de equilibrio
def DA_C(Co, Io, Go, Xo, h, r, b, m, t, g, Y):
DA_C = (Co + Io + Go + Xo - h*r) + [(b-m)*(1-t)-g]*Y
return DA_C
DA_Cont = DA_C(Co, Io, Go, Xo, h, r, b, m, t, g, Y)
# Nueva curva
Xo = 1
def DA_C(Co, Io, Go, Xo, h, r, b, m, t, g, Y):
DA_C = (Co + Io + Go + Xo - h*r) + [(b-m)*(1-t)-g]*Y
return DA_C
DA_C_X = DA_C(Co, Io, Go, Xo, h, r, b, m, t, g, Y)
# líneas punteadas autómaticas
# definir la función line_intersection
def line_intersection(line1, line2):
xdiff = (line1[0][0] - line1[1][0], line2[0][0] - line2[1][0])
ydiff = (line1[0][1] - line1[1][1], line2[0][1] - line2[1][1])
def det(a, b):
return a[0] * b[1] - a[1] * b[0]
div = det(xdiff, ydiff)
if div == 0:
raise Exception('lines do not intersect')
d = (det(*line1), det(*line2))
x = det(d, xdiff) / div
y = det(d, ydiff) / div
return x, y
# coordenadas de las curvas (x,y)
A = [DA_Cont[0], Y[0]] # DA, coordenada inicio
B = [DA_Cont[-1], Y[-1]] # DA, coordenada fin
C = [L_45[0], Y[0]] # L_45, coordenada inicio
D = [L_45[-1], Y[-1]] # L_45, coordenada fin
# creación de intersección
intersec = line_intersection((A, B), (C, D))
intersec # (y,x)
(174.7478070175439, 69.89912280701755)
# coordenadas de las curvas (x,y)
A = [DA_C_X[0], Y[0]] # DA, coordenada inicio
B = [DA_C_X[-1], Y[-1]] # DA, coordenada fin
C = [L_45[0], Y[0]] # L_45, coordenada inicio
D = [L_45[-1], Y[-1]] # L_45, coordenada fin
# creación de intersección
intersec_X = line_intersection((A, B), (C, D))
intersec_X # (y,x)
(159.39692982456143, 63.75877192982457)
# Gráfico
y_max = np.max(DA_Cont)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(DA_Cont, label = "DA", color = "#3D59AB") #curva ORIGINAL
ax.plot(DA_C_X, label = "DA_X", color = "#EE7600", linestyle = 'dashed') #NUEVA curva
ax.plot(L_45, color = "#404040") #línea de 45º
# Lineas punteadas
plt.axhline(y=intersec[0], xmin= 0, xmax= 0.68, linestyle = ":", color = "grey")
plt.axvline(x=intersec[1], ymin= 0, ymax= 0.68, linestyle = ":", color = "grey")
plt.axhline(y=intersec_X[0], xmin= 0, xmax= 0.63, linestyle = ":", color = "grey")
plt.axvline(x=intersec_X[1], ymin= 0, ymax= 0.63, linestyle = ":", color = "grey")
# Texto agregado
plt.text(0, 180, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(0, 135, '$DA_X$', fontsize = 11.5, color = '#EE7600')
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
plt.text(71, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(60, 0, '$Y_X$', fontsize = 12, color = '#EE7600')
plt.text(65.5, 45, '$←$', fontsize = 15, color = 'grey')
plt.text(20, 165, '$↓$', fontsize = 15, color = 'grey')
# Título y leyenda
ax.set(title = "Reducción de las Exportaciones", xlabel = r'Y', ylabel = r'DA')
ax.legend()
plt.show()
